Scale, by Geoffrey West, is a thought provoking book about coarse grained quantitative network theories which concern the entire human species and its interaction with the environment. Although verbose — as I think the intended audience is upper high school and entry-level college — it is clear in its depictions and explanations. This book is an important summary of really profound work and research performed at the Santa Fe Institute. And it is a great introduction to understanding power laws and scaling in biology and network topologies.
Category: geoffrey west (Page 1 of 2)
Hidden Forces, hosted by Demetri Kofinas is an nice set of interviews with various people on topics including: finance, complexity, mathematics, and cryptocurrencies. I struggled listening to some of the interviewees because I did not agree with their ideas or conclusions; but I guess it is good to have conflicting opinions in order to encourage debate in the comments and to help review one’s own opinions and understandings. Regardless, Kofinas provides a highly accessible medium through which advanced ideas can be grasped.
I first ran across Hidden Forces while listening to the interview with Ray Monk about philosophical mathematics. Monk’s narration on the work of Frege, Russell, Whitehead, Wittgenstein, and Gödel is excellent – by far one of the clearest and easiest to grasp. It was learning about these paradigms and paradoxes of mathematics via Hofstadter’s famous book which led me to start this website.
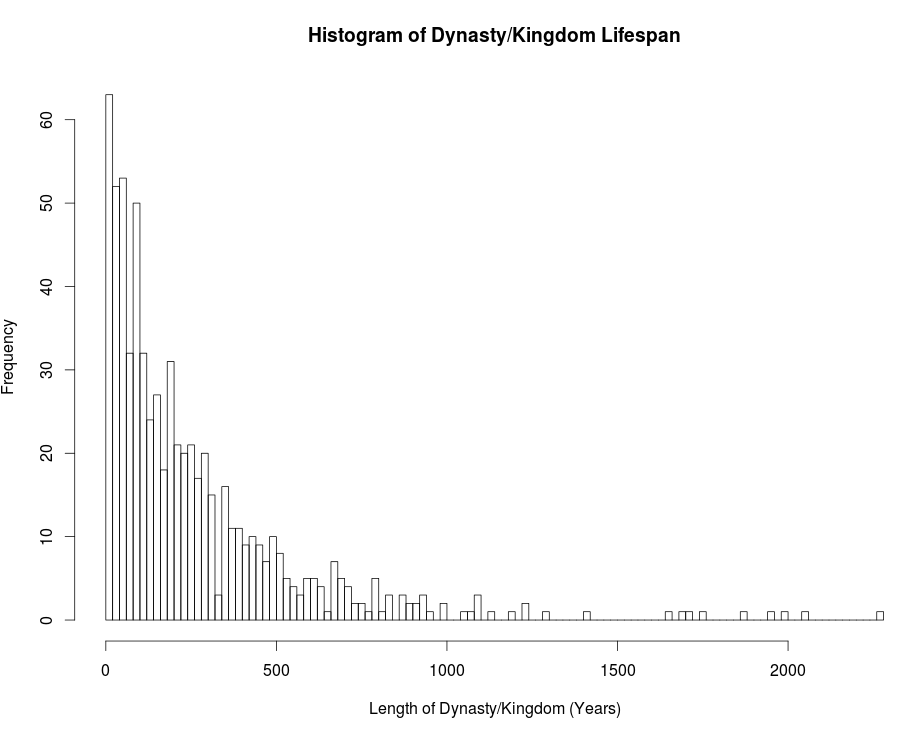
Do there exist studies on the distribution of the lengths of kingdoms and dynasties — distinct political entities — since the 3rd millennium B.C.E.? It seems likely that someone has already studied this topic, but I can not find any papers online. To explain, I have included a file, here, containing the beginning and end dates of about 700 distinct social groups since the dawn of recorded history. It was complied from various Wikipedia pages. I do not doubt that the data is not very reliable, however, graphing the histogram of these lengths, see Figure 1, would provide at least a rough idea of their distribution.
 |
| Figure 1 |
It does seem that a nice distribution curve exists which models the data. The distribution seems to take the shape of a power law at first glance. Doing some work in R, I found that a power law with one set of parameters fits the tail nicely but fails to fit the first half; and vice versa, a power law with a different set of parameters fits the majority but not the tail. My hypothesis is that a power law with alpha equal to 3 may be the best fit. This is a prediction based on the lectures of Geoffrey West, in which he explains that most biological systems exhibit power law distributions with alpha in the 2.5-3.0 range. However, as seen in Figure 2, this does not seem to be the correct range for alpha if a power law is the best fit for this preliminary data.
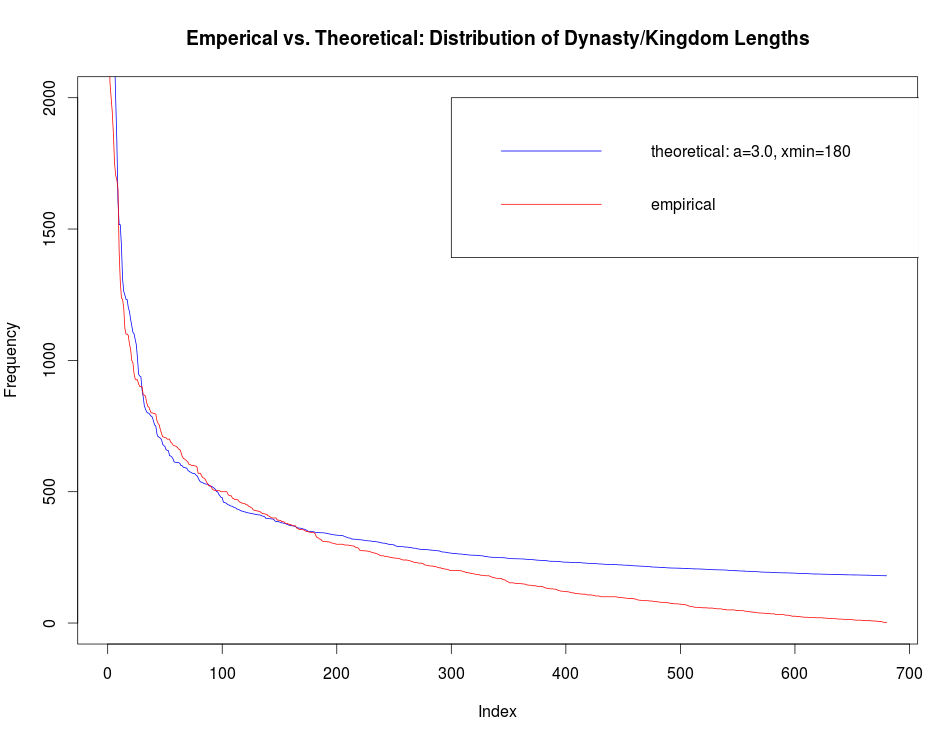 |
| Figure 2 |




